为什么需要池化层
基于前面写的卷积,这一节来讲讲池化层,同样是一个很简单的概念。可以理解为为了减小卷积层对于图像位置的敏感,采用了池化层。
那么为什么卷积层会对位置敏感呢?我们看看这幅图:
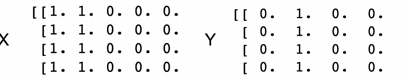
这是我们之前在卷积层里讲过的,边缘处理问题,通过一个一位张量就可以实现黑白图片的边缘识别,但是真实的图片的像素不是固定不动的,可能会随着照明,物体位置,外观比例等因素变化,所以我们需要一定的平移不变性,从而使图片产生细微变化时,我们的输出仍然保持不变。
最大池化层和平均池化层
池化层也是通过滑动窗口的方式实现的,但卷积是通过二维互相关运算实现的,池化层则非常简单,只是通过求窗口内的最大值和平均值来实现的。
现在我们以最大池化层的实现举例,平均池化层也可推广:
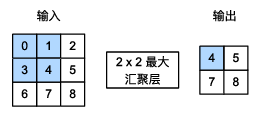
非常简单的运算形式,如下:
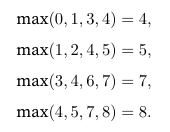
代码实现
import torch
from torch import nn
def pool2d(X,pool_size,mode='max'):
'''
对二维输入数据进行池化操作
参数:
X: 二维输入张量
pool_size: 池化窗口大小,格式为(高度, 宽度)
mode: 池化模式,'max'表示最大池化,'avg'表示平均池化,默认为'max'
返回值:
Y: 池化后的二维输出张量
'''
p_h,p_w=pool_size
# 创建输出张量,大小根据输入张量和池化窗口大小计算得出
Y=torch.zeros((X.shape[0]-p_h+1,X.shape[1]-p_w+1))
# 遍历输出张量的每个位置,计算对应的池化值
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode=='max':
Y[i,j]=X[i:i+p_h,j:j+p_w].max()
elif mode=='avg':
Y[i,j]=X[i:i+p_h,j:j+p_w].mean()
return Y
X=torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
print(pool2d(X,(2,2)))
print(pool2d(X,(2,2),'avg'))
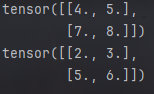
可以看到运行结果符合预期:
填充和步幅
上一节我们学习了卷积层里的填充和步幅,池化层里的填充和步幅同样是用来实现输入和输出的一致的。我们使用深度学习的框架中内置的二维最大池化层,来演示池化层里的填充和步幅的使用,
我们首先构造一个张量X,四个维度分别是样本数,通道数,高度和宽度:
X=torch.arange(16,dtype=torch.float32).reshape(1,1,4,4)
print(X)
结果是:
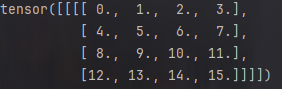
默认情况下,深度学习框架中的步幅与汇聚窗口的大小相同,比如我们使用一个(3,3)的汇聚窗口,步幅也为(3,3) :
pool2d=nn.MaxPool2d(3)
print(pool2d(X))
结果自然是:

因为水平和垂直步幅都为3,所以只有第一次可以池化。
填充和步幅可以手动设定:
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
print(pool2d(X))
结果为:
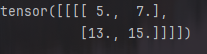
大小也可以设定:
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
print(pool2d(X))
结果与上同。
多通道
池化层建立多通道时和卷积不同,卷积的多通道分别运算之后汇总,而池化层的输入通道和输出通道数相同,例子如下,我们在通道维度上连结两个张量,构成两个通道的输入:
X = torch.cat((X, X + 1), 1)
print(X)
结果如下:
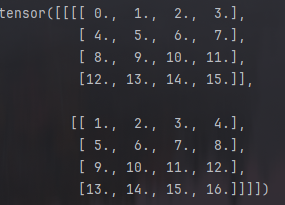
汇聚后的输出通道仍然是2:
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
print(pool2d(X))
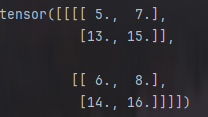
 网硕互联帮助中心
网硕互联帮助中心






评论前必须登录!
注册