深度学习：PyTorch自动微分模块

本文目录：

• 一、自动微分相关概念
• 二、梯度基本计算
• • （一）标量张量梯度计算
  • （二）向量张量梯度计算
• 三、梯度下降法求最优解
• 四、梯度计算注意点
• 五、自动微分模块应用
• 六、PyTorch构建线性回归模型
• • （一）流程
  • （二）代码实现

一、自动微分相关概念

自动微分就是自动计算梯度值，也就是计算导数。 训练神经网络时，最常用的算法就是反向传播。在该算法中，参数（模型权重）会根据损失函数关于对应参数的梯度进行调整。为了计算这些梯度，PyTorch内置了名为 torch.autograd 的微分模块。它支持任意计算图的自动梯度计算：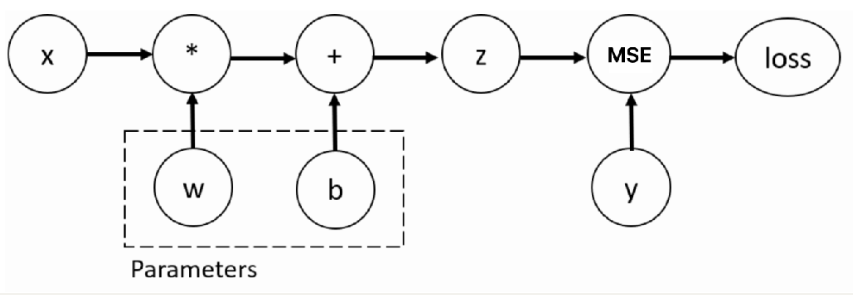

二、梯度基本计算

• pytorch不支持向量张量对向量张量的求导,只支持标量张量对向量张量的求导
• x如果是张量,y必须是标量(一个值)才可以进行求导；
• 计算梯度: y.backward(), y是一个标量，实际常常使用y.sum()以改变y的张量性质；
• 获取x点的梯度值: x.grad, 会累加上一次的梯度值。

（一）标量张量梯度计算

# 定义一个标量张量(点)
# requires_grad=:默认为False,不会自动计算梯度;为True的话是将自动计算的梯度值保存到grad中
x = torch.tensor(10, requires_grad=True, dtype=torch.float32)
print("x–>", x)

# 定义一个曲线
y = 2 * x ** 2
print("y–>", y)
# 查看梯度函数类型,即曲线函数类型，简单来说了解y是怎么来的，比如y=sum(x)，就返回sum相关操作
print(y.grad_fn)

# 计算x点的梯度
# 此时y是一个标量,可以不用使用y.sum()转换成标量
print("y.sum()–>", y.sum())
# y'|(x=10) = (2*x**2)'|(x=10) = 4x|(x=10) = 40
y.backward()

# 打印x的梯度值
print("x的梯度值是:", x.grad)

（二）向量张量梯度计算

# 定义一个向量张量(点)
x = torch.tensor([10, 20], requires_grad=True, dtype=torch.float32)
print("x–>", x)

# 定义一个曲线
y = 2 * x ** 2
print("y–>", y)

# 计算梯度
# x和y都是向量张量,不能进行求导,需要将y转换成标量张量–>y.sum()
# y'|(x=10) = (2*x**2)'|(x=10) = 4x|(x=10) = 40
# y'|(x=20) = (2*x**2)'|(x=20) = 4x|(x=20) = 80
y.sum().backward()

# 打印x的梯度
print("x.grad–>", x.grad)

三、梯度下降法求最优解

梯度下降法公式: w = w – r * grad (r是学习率, grad是梯度值) 清空上一次的梯度值: x.grad.zero_()

# 需求：求 y = x**2 + 20 的极小值点 并打印y是最小值时 w的值(梯度)
# 1 定义点 ：x=10 requires_grad=True dtype=torch.float32
# 2 定义函数： y = x**2 + 20
# 3 利用梯度下降法 循环迭代1000 求最优解
# 3-1 正向计算(前向传播)
# 3-2 梯度清零 ：x.grad.zero_()
# 3-3 反向传播
# 3-4 梯度更新： x.data = x.data – 0.01 * x.grad

# 1 定义点：x=10 requires_grad=True dtype=torch.float32
x = torch.tensor(10, requires_grad=True, dtype=torch.float32)

# 2 定义函数 y = x ** 2 + 20
y = x ** 2 + 20
print('开始 权重x初始值:%.2f (0.01 * x.grad):无 y:%.2f' % (x, y))

# 3 利用梯度下降法 循环迭代1000 求最优解
for i in range(1, 1001):

# 3-1 正向计算(前向传播)
y = x ** 2 + 20

# 3-2 梯度清零：x.grad.zero_()
# 张量的 grad 属性默认会累加历史梯度值，需手工清零上一次的提取
# 一开始梯度不存在, 需要做判断
if x.grad is not None:
x.grad.zero_() #梯度清零

# 3-3 反向传播
y.sum().backward() #也可不加sum()

# 3-4 梯度更新 x.data = x.data – 0.01 * x.grad
# x.data是修改原始x内存中的数据,前后x的内存空间一样;如果使用x,此时修改前后x的内存空间不同
x.data = x.data – 0.01 * x.grad # 注：不能 x = x – 0.01 * x.grad 这样写

print('次数:%d 权重x: %.6f, (0.01 * x.grad):%.6f y:%.6f' % (i, x, 0.01 * x.grad, y))

print('x：', x, x.grad, 'y最小值:', y)

四、梯度计算注意点

若张量设置了梯度跟踪，便不可直接转换成numpy数组，会发生报错，需要通过detach()方法先“引用传递”数据，再转换。

# 定义一个张量
x1 = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64) #设置了梯度跟踪：requires_grad=True

# 将x张量转换成numpy数组
# 发生报错：RuntimeError: Can't call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.
# 不能将自动微分的张量转换成numpy数组
# print(x1.numpy())

# 通过detach()方法产生一个新的张量,作为叶子结点
x2 = x1.detach() #相当于x1数据引用传递到x2
# x1和x2张量共享数据,但是x2不会自动微分
print(x1.requires_grad) #结果为True
print(x2.requires_grad) #结果为False
# x1和x2张量的值一样,共用一份内存空间的数据
print(x1.data)
print(x2.data) #x1和x2数据一样
print(id(x1.data))
print(id(x2.data)) #x1和x2的id一样，说明共用同一份内存数据

# 将x2张量转换成numpy数组
print(x2.numpy()) #可行

五、自动微分模块应用

import torch
#下面定义x，y，w，b，需要注意x，y，w和b行列数符合矩阵运算和损失函数运算标准
# 输入张量 2*5
x = torch.ones(2, 5)
# 目标值是 2*3
y = torch.zeros(2, 3)
# 设置要更新的权重和偏置的初始值
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
# 设置网络的输出值
z = torch.matmul(x, w) + b # 矩阵乘法
# 设置损失函数，并进行损失的计算
loss = torch.nn.MSELoss()
loss = loss(z, y)
# 自动微分
loss.backward()
# 打印 w,b 变量的梯度
# backward 函数计算的梯度值会存储在张量的 grad 变量中
print("W的梯度:", w.grad)
print("b的梯度", b.grad)

六、PyTorch构建线性回归模型

（一）流程

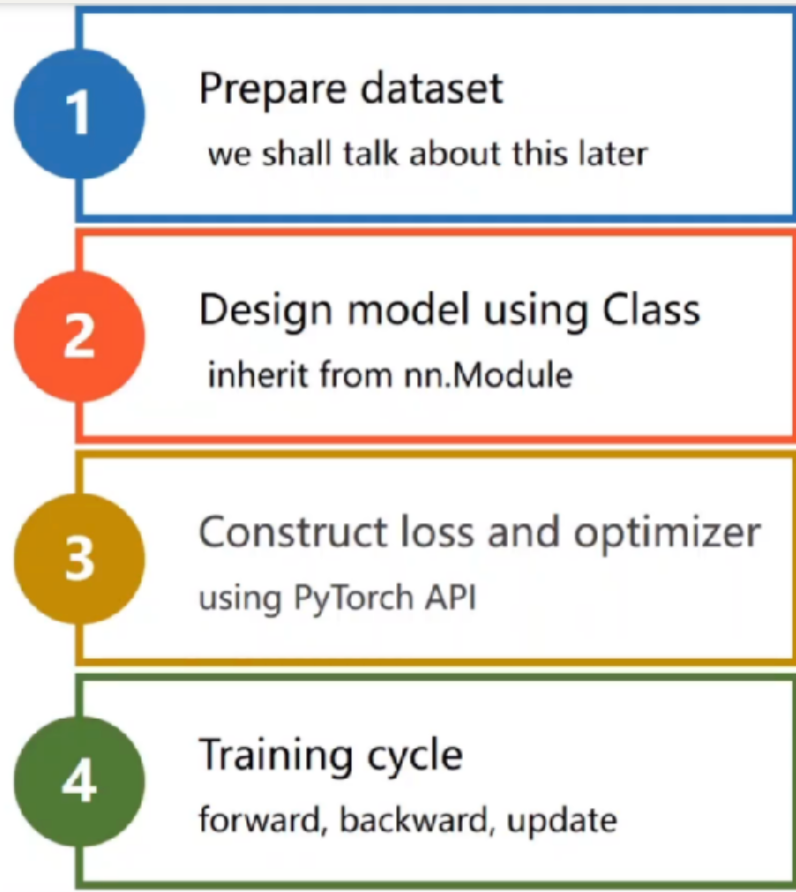总共四个步骤（翻译自上文）：

（二）代码实现

import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt
from sklearn.datasets import make_regression
from torch.utils.data import TensorDataset

def create_dataset():
"""
生成数据集

Returns:
x (torch.Tensor): 输入特征张量
y (torch.Tensor): 目标值张量
coef (float): 回归系数
"""
x, y, coef = make_regression(n_samples=100, n_features=1, bias=14.5, noise=5, coef=True)
x = torch.tensor(x, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32).unsqueeze(1)
return x, y, coef

def train_model(x, y, epochs):
"""
训练模型

Args:
x (torch.Tensor): 输入特征张量
y (torch.Tensor): 目标值张量
epochs (int): 训练轮数
"""
dataset = TensorDataset(x, y)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True) #数据加载器
model = nn.Linear(1, 1) #定义一个最简单的全连接层（线性层）
criterion = nn.MSELoss() #损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01) #优化器
epoch_loss, total_loss, train_sample = [], 0, 0 #初始化
for epoch in range(epochs): #定义轮次
for batch_x, batch_y in dataloader: #按批次，一批次10个（batch_size）
pre_y = model(batch_x)
loss = criterion(pre_y, batch_y)
total_loss += loss.item()
train_sample += len(batch_x)
optimizer.zero_grad() #每批次梯度清零，否则默认累加
loss.sum().backward() #自动微分
optimizer.step()
epoch_loss.append(total_loss / train_sample)
print(f'model.weights:{model.weight},model.bias:{model.bias}')
"""
绘制训练损失和预测图

Args:
epochs (int): 训练轮数
epoch_loss (list): 每轮训练的损失
x (torch.Tensor): 输入特征张量
y (torch.Tensor): 目标值张量
coef (float): 回归系数
model (nn.Module): 训练好的模型
"""
fig, ax = plt.subplots(2, 1)
ax[0].plot(range(epochs), epoch_loss) #损失值与轮次关系
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].set_title('loss')

x = x.squeeze(1).numpy()
y = y.squeeze(1).numpy()

ax[1].scatter(x, y) # x,y不降维也可以画图：观测值散点图

x = torch.linspace(-3, 3, 100)
y_pred = torch.tensor([model.weight * i + model.bias for i in x]) #预测回归线
y_true = torch.tensor([coef * i + 14.5 for i in x.numpy()]) #理想回归线
ax[1].plot(x, y_pred, label='prediction', color='red')
ax[1].plot(x, y_true, label='true', color='green')
ax[1].legend() #图例
ax[1].grid(True) #网格
ax[1].set_title('prediction and true') #标题
plt.tight_layout() # 自动调整子图和标签间距
plt.show()

if __name__ == '__main__':
epochs = 100
x, y, coef = create_dataset()
train_model(x, y, epochs)

输出图像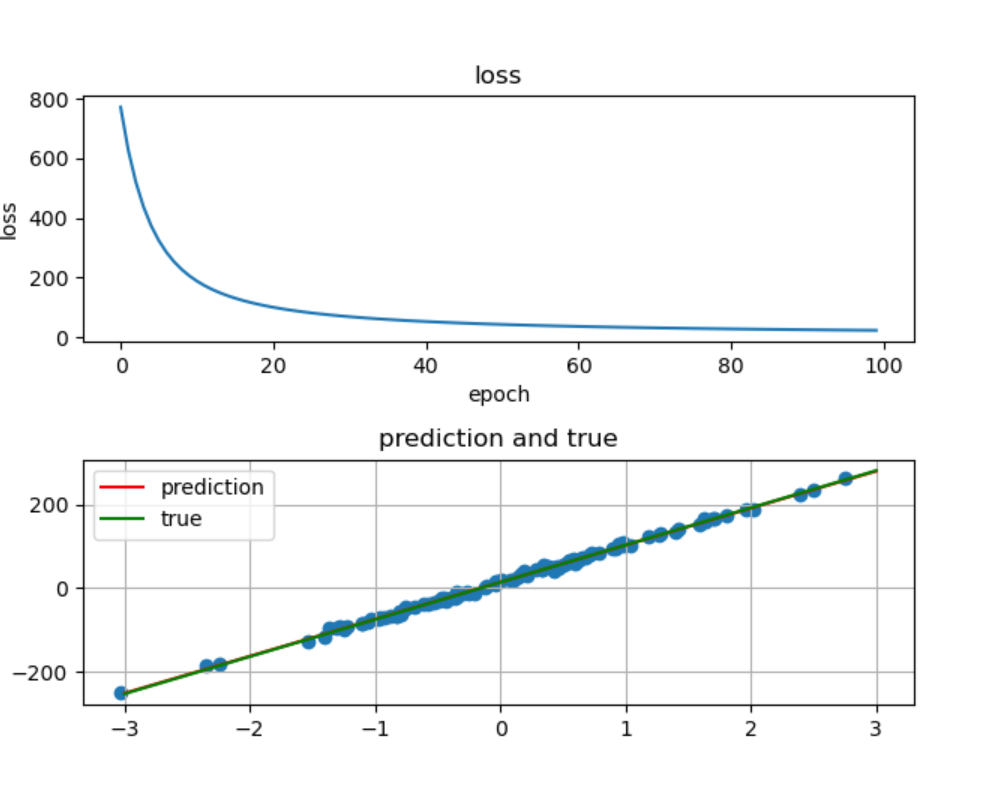： 今日分享到此结束。