蓝桥杯刷题——第十五届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组

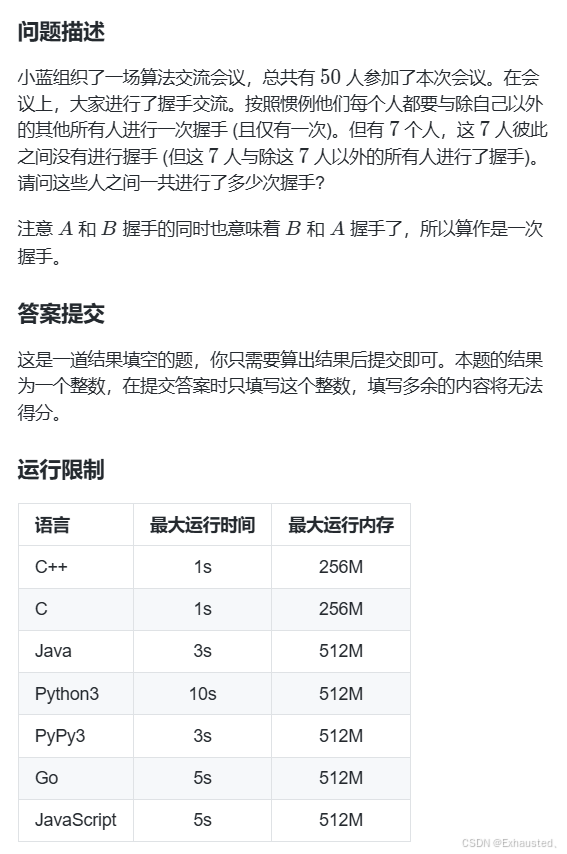
一、0握手问题 – 蓝桥云课

算法代码：

#include <iostream>
using namespace std;
int main()
{
int sum=0;
for(int i=49;i>=7;i–)
sum+=i;
cout<<sum<<endl;
return 0;
}

直接暴力，题意很清晰，累加即可。 

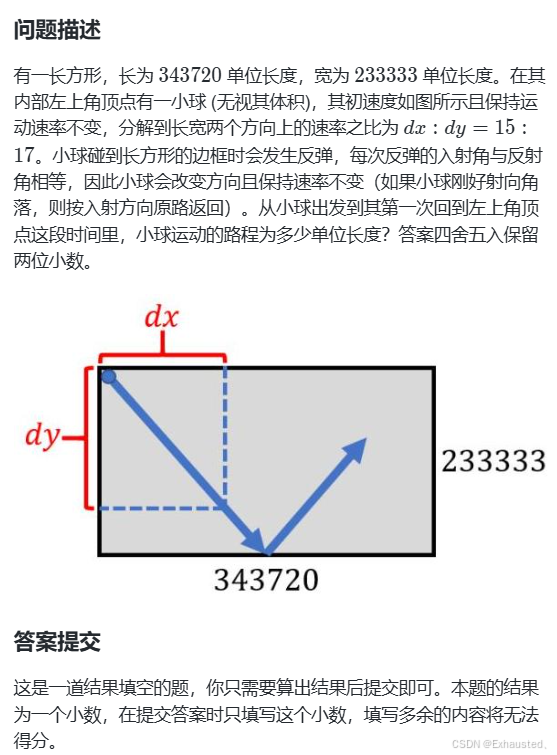
二、0小球反弹 – 蓝桥云课

算法代码： 

#include<iostream> // 引入输入输出流库，用于标准输入输出操作
#include<iomanip> // 引入输入输出操纵库，用于格式化输出（如设置小数点精度）
#include<cmath> // 引入数学函数库，用于数学运算（如平方根）

using namespace std; // 使用标准命名空间，避免每次调用标准库函数时都要加std::

// 定义一个函数check，用于检查两个整数a和b是否满足特定条件
bool check(int a, int b) {
// 如果a能被b整除，并且a除以b的结果是偶数，则返回true
if (a % b == 0 && (a / b) % 2 == 0) return true;
return false; // 否则返回false
}

// 主函数
int main() {
long long x = 343720, y = 233333; // 定义两个长整型变量x和y，并赋予初始值
long long t = 1; // 定义长整型变量t，并初始化为1
long long lx, ly; // 定义两个长整型变量lx和ly，用于存储计算过程中的临时值

// 进入一个无限循环，直到满足特定条件时跳出循环
while (1) {
lx = 15 * t; // 计算lx为15乘以t
ly = 17 * t; // 计算ly为17乘以t

// 如果lx和x满足check函数的条件，且ly和y也满足check函数的条件，则跳出循环
if (check(lx, x) && check(ly, y)) break;

t++; // 否则，t自增1，继续循环
}

// 输出lx和ly的平方和的平方根，保留两位小数
cout << setprecision(2) << fixed << sqrt(lx * lx + ly * ly);

return 0; // 程序正常结束，返回0
}

问题背景

数学分析

setprecision(2) 是 C++ 标准库 <iomanip> 中的一个操纵符，用于设置浮点数输出的精度。具体来说，它控制输出流中浮点数的小数点后的位数。

详细解释

• setprecision(n)：设置浮点数输出的小数点后的位数为 n。例如，setprecision(2) 表示输出浮点数时保留两位小数。

• fixed：与 setprecision 结合使用，表示使用固定小数格式输出。这意味着小数点后的位数是固定的，而不是科学计数法。

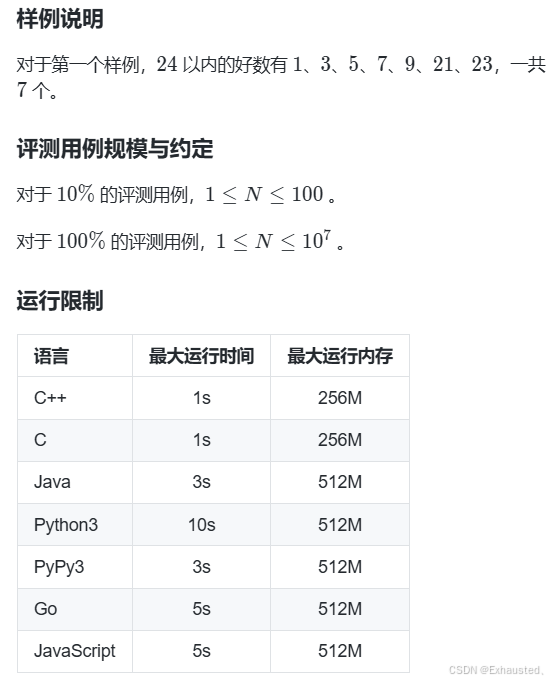
三、0好数 – 蓝桥云课 

算法代码：

#include <stdio.h>
int main()
{
int n, i;
scanf("%d", &n); // 输入一个整数 n
for (; n > 0; n–) // 从 n 开始，递减到 1
{
for (int m = n; m > 0;) // 对每个数字 m = n，检查其每一位
{
if (m % 2 != 0) m /= 10; // 如果最低位是奇数，去掉最低位
else break; // 如果最低位是偶数，退出循环
if (m % 2 == 0) m /= 10; // 如果新的最低位是偶数，去掉最低位
else break; // 如果新的最低位是奇数，退出循环
if (m == 0) i++; // 如果 m 变为 0，说明满足条件，计数器 i 增加
}
}
printf("%d", i); // 输出满足条件的数字的数量
return 0;
}

        题意清晰，直接一个一个数地循环递减，然后按规则，直接判断奇数位和偶数位是不是符合条件。

四、0R 格式 – 蓝桥云课

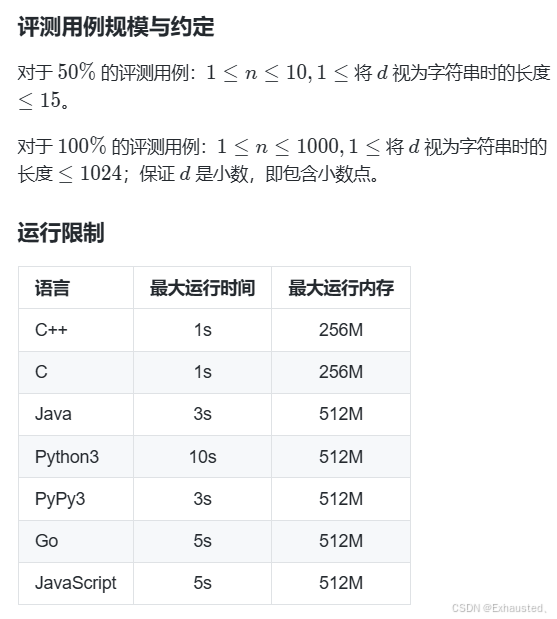
自己写的：算法代码（只能通过50%的测试用例） 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

// 快速幂函数，计算 2^n
ll fastPow(int n) {
ll a = 2; // 底数为 2
ll sum = 1; // 初始化 sum 为 1
while (n) {
if (n & 1) {
sum = sum * a; // 如果当前位为 1，累乘到 sum
}
a = a * a; // 底数平方
n >>= 1; // 右移一位
}
return sum;
}

int main() {
int n;
double d;
cin >> n >> d; // 输入 n 和 d
ll ans = fastPow(n); // 计算 2^n
ll end_format = round(d * ans); // 将 d 乘以 2^n 并四舍五入
//round 函数用于对浮点数进行四舍五入操作
printf("%lld\\n", end_format); // 输出结果
return 0;
}

 罗勇军老师的几行代码（50%）（高下立判了属于是哈哈）算法代码：

#include <bits/stdc++.h>
using namespace std;
int main()
{    
long long n;    
double s;   
cin>>n>>s;    
long long  a = 1<<n;    
long long b= (long long)(a*s*1.0+0.5);//加0.5四舍五入   
cout << b;
}

题解：

#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std; // 使用标准命名空间

int main()
{
int n;
string d; // 由于数字可能非常大，使用字符串来读取
cin >> n >> d; // 输入转换参数 n 和浮点数 d

vector<int> b; // 使用 vector 来存储数字的每一位，方便处理进位
int sum = 0, k = 0; // sum 用于记录总位数，k 用于记录小数点的位置

// 从字符串末尾开始遍历，将字符转换为整数并存储到 vector 中
for(int i = d.size() – 1; i >= 0; i–)
{
if(d[i] != '.')
b.push_back(d[i] – '0'); // 将字符转换为整数并存储
else {
k = sum; // 记录小数点的位置
}
sum++; // 记录总位数
}

int u = b.size(); // 记录当前数字的位数

// 进行 n 次乘以 2 的操作
while(n–)
{
int t = 0; // t 用于记录进位
for(int i = 0; i < b.size(); i++)
{
b[i] = b[i] * 2 + t; // 当前位乘以 2 并加上进位
if(b[i] >= 10)
{
t = b[i] / 10; // 计算新的进位
b[i] = b[i] % 10; // 取余数作为当前位的值
}
else {
t = 0; // 如果没有进位，置为 0
}
}
if(t) // 如果最后还有进位，添加到 vector 中
b.push_back(t);
}

u = b.size(); // 更新数字的位数

int t = 1; // 用于处理四舍五入的进位
if(k && b[k – 1] >= 5) // 如果需要四舍五入
{
for(int i = k; i < u; i++)
{
b[i] = b[i] + 1; // 当前位加 1
if(b[i] <= 9) { // 如果不需要继续进位
t = 0;
break;
}
else {
b[i] -= 10; // 如果需要继续进位
}
}
if(t) // 如果最后还有进位，添加到 vector 中
b.push_back(t);
}

// 从最高位开始输出结果，忽略小数部分
for(int i = b.size() – 1; i >= k; i–)
cout << b[i];

return 0; // 程序结束
}

1. 输入处理

• 输入：读取整数 n 和浮点数 d。

  • n 是转换参数，表示需要将浮点数乘以 2^n。

  • d 是待转换的浮点数，可能非常大，因此用字符串存储。

• 目标：将浮点数 d 转换为整数形式，方便后续计算。

2. 将浮点数转换为整数形式

• 遍历浮点数字符串：

  • 从字符串末尾开始遍历，将每个数字字符转换为整数，并存储到 vector<int> b 中。

  • 如果遇到小数点 .，记录小数点的位置 k，表示小数点后有 k 位。

• 结果：

  • b 中存储的是浮点数 d 的整数形式（去掉小数点）。

  • k 记录了小数点的位置，用于后续四舍五入。

3. 高精度乘以 2^n

• 循环乘以 2：

  • 进行 n 次乘以 2 的操作，每次操作都模拟高精度乘法。

  • 每次乘以 2 时，遍历 b 中的每一位，计算当前位乘以 2 并加上进位。

  • 如果当前位的结果大于等于 10，则计算进位，并将当前位的结果取余。

  • 如果最后还有进位，将其添加到 b 的末尾。

• 结果：

  • b 中存储的是浮点数 d 乘以 2^n的结果，仍然是一个高精度整数。

4. 四舍五入

• 判断是否需要四舍五入：

  • 根据小数点的位置 k，检查小数点后的第一位（即 b[k-1]）是否大于等于 5。

  • 如果大于等于 5，则需要进行四舍五入。

• 四舍五入操作：

  • 从小数点位置开始，向高位逐位加 1，直到没有进位为止。

  • 如果最高位仍有进位，将其添加到 b 的末尾。

• 结果：

  • b 中存储的是四舍五入后的最终结果。

5. 输出结果

• 从最高位开始输出：

  • 从 b 的最高位开始，输出每一位数字。

  • 忽略小数部分（即小数点后的位数）。

• 结果：

  • 输出的是浮点数 d 乘以 2^n 并四舍五入后的整数结果。

6. 代码的核心思想

• 高精度计算：

  • 由于浮点数和 2^n 可能非常大，普通数据类型无法存储，因此使用字符串和 vector<int> 来模拟高精度计算。

• 逐位处理：

  • 通过逐位遍历和进位处理，实现了高精度乘法和四舍五入。

• 四舍五入：

  • 根据小数点后的第一位决定是否需要进位，模拟了四舍五入的过程。

五、 0宝石组合 – 蓝桥云课

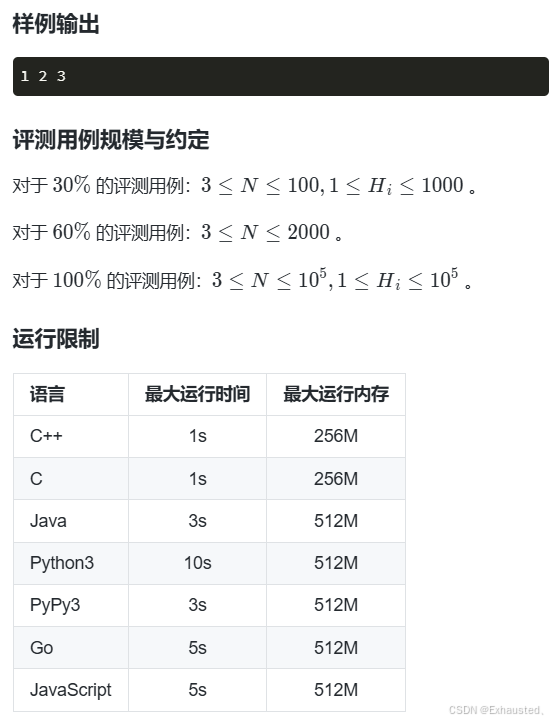
（这道题我只会暴力，而且没拿到该拿的分，别提了，都是泪）

牛逼的题解：

#include <bits/stdc++.h> // 包含所有标准库头文件

#define N 500010 // 定义常量 N，表示数组的最大大小

int gem[N], num[N]; // 定义两个数组：gem 用于存储输入的宝石编号，num 用于统计每种宝石的数量

int main() {
int n;
scanf("%d", &n); // 输入整数 n，表示宝石的数量

int max = -0x3f3f3f3f; // 初始化 max 为一个很小的值，用于记录宝石编号的最大值
for (int i = 0; i < n; i++) {
scanf("%d", &gem[i]); // 输入每个宝石的编号
num[gem[i]]++; // 统计每种宝石的数量
if (gem[i] > max) max = gem[i]; // 更新宝石编号的最大值
}

// 从最大值开始，尝试找到满足条件的三个宝石
for (int i = max; i >= 1; i–) { // i 是可能的公因数
int tmp[3], pos = 0; // tmp 用于存储符合条件的宝石编号，pos 用于记录 tmp 中的位置
int cnt = 0; // cnt 用于统计符合条件的宝石数量

// 遍历所有 i 的倍数，检查是否存在对应的宝石
for (int j = i; j <= max; j += i) { // j 是 i 的倍数
if (num[j]) { // 如果宝石 j 存在
cnt += num[j]; // 统计宝石 j 的数量
for (int k = 0; k < num[j] && pos < 3; k++) { // 将宝石 j 加入 tmp
tmp[pos++] = j;
}
}
if (cnt == 3) break; // 如果找到三个宝石，跳出循环
}

// 如果找到三个宝石，输出结果并结束程序
if (cnt == 3) {
for (int j = 0; j < 3; j++) {
printf("%d ", tmp[j]); // 输出三个宝石的编号
}
break; // 结束程序
}
}

return 0; // 程序结束
}

代码思路： 

六、0数字接龙 – 蓝桥云课 

题解代码：

#include <bits/stdc++.h> // 包含所有标准库头文件
using namespace std;

const int N = 11; // 定义棋盘的最大大小为11×11
int n, k; // n为棋盘大小，k为数字循环的范围
int g[N][N]; // 存储棋盘上的数字
int dx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}; // 定义8个方向的x坐标偏移
int dy[8] = {0, 1, 1, 1, 0, -1, -1, -1}; // 定义8个方向的y坐标偏移
string path; // 存储路径的方向编号
bool st[N][N]; // 标记棋盘上的格子是否被访问过
bool edge[N][N][N][N]; // 检查路径是否交叉

// 深度优先搜索函数，用于寻找路径
bool dfs(int a, int b) {
// 如果到达右下角格子，检查路径长度是否为n*n-1（因为起点不计入路径）
if (a == n – 1 && b == n – 1)
return path.size() == n * n – 1;

st[a][b] = true; // 标记当前格子已访问
for (int i = 0; i < 8; i++) { // 遍历8个方向
int x = a + dx[i], y = b + dy[i]; // 计算目标格子的坐标
// 检查目标格子是否越界、是否访问过、数字是否满足循环序列要求
if (x < 0 || x >= n || y < 0 || y >= n) continue;
if (st[x][y]) continue;
if (g[x][y] != (g[a][b] + 1) % k) continue;
// 检查路径是否交叉（对于斜向移动，检查是否有反向的路径）
if (i % 2 && (edge[a][y][x][b] || edge[x][b][a][y])) continue;

edge[a][b][x][y] = true; // 标记路径
path += i + '0'; // 将方向编号加入路径
if (dfs(x, y)) return true; // 递归搜索下一个格子
path.pop_back(); // 回溯，移除路径中的最后一个方向
edge[a][b][x][y] = false; // 回溯，取消路径标记
}
st[a][b] = false; // 回溯，取消当前格子的访问标记
return false; // 如果所有方向都无法到达终点，返回false
}

int main() {
cin >> n >> k; // 输入棋盘大小和数字循环范围
for (int i = 0; i < n; i++) // 读取棋盘上的数字
for (int j = 0; j < n; j++)
cin >> g[i][j];

// 从起点(0,0)开始搜索路径
if (!dfs(0, 0))
cout << -1 << endl; // 如果没有找到路径，输出-1
else
cout << path << endl; // 输出路径的方向编号序列

return 0;
}

罗勇军老师的分析：（有道理）

七、0拔河 – 蓝桥云课

算法代码（20%暴力枚举） 

//20%：暴力枚举
#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std; // 使用标准命名空间

const int N = 1e3 + 100; // 定义常量 N，表示数组的最大大小
typedef long long ll; // 定义 long long 类型的别名 ll
ll a[100]; // 定义数组 a，用于存储输入的数字

// 计算子数组和的函数
ll sum(int l, int r) {
ll s = 0; // 初始化子数组和为 0
for (int i = l; i <= r; i++) // 遍历子数组的每个元素
s += a[i]; // 累加子数组的元素
return s; // 返回子数组的和
}

int main() {
int n; // 定义整数 n，表示数组的大小
cin >> n; // 输入数组的大小 n

for (int i = 1; i <= n; i++) // 遍历数组的每个位置
cin >> a[i]; // 输入数组的每个元素

ll ans = 1e12; // 初始化答案为一个大值（1e12），用于存储最小绝对差

// 暴力枚举所有可能的子数组对
for (int l1 = 1; l1 <= n; l1++) { // 枚举第一个子数组的起始位置 l1
for (int r1 = l1; r1 <= n; r1++) { // 枚举第一个子数组的结束位置 r1
for (int l2 = r1 + 1; l2 <= n; l2++) { // 枚举第二个子数组的起始位置 l2
for (int r2 = l2; r2 <= n; r2++) { // 枚举第二个子数组的结束位置 r2
// 计算两个子数组和的绝对差，并更新最小值
ans = min(ans, abs(sum(l2, r2) – sum(l1, r1)));
}
}
}
}

cout << ans; // 输出最小绝对差
return 0; // 程序结束
}

 算法代码（40%暴力枚举+前缀和优化） 

#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std; // 使用标准命名空间

const int N = 1e3 + 100; // 定义常量 N，表示数组的最大大小
typedef long long ll; // 定义 long long 类型的别名 ll
ll a[N], prefix[N]; // 定义数组 a 和前缀和数组 prefix

// 计算子数组和的函数
ll sum(int l, int r) {
return prefix[r] – prefix[l – 1]; // 返回子数组 [l, r] 的和
}

int main() {
int n; // 定义整数 n，表示数组的大小
cin >> n; // 输入数组的大小 n

// 读取数组并计算前缀和
for (int i = 1; i <= n; i++) {
cin >> a[i]; // 输入数组的每个元素
prefix[i] = prefix[i – 1] + a[i]; // 计算前缀和
}

ll ans = 1e12; // 初始化答案为一个大值（1e12），用于存储最小绝对差

// 枚举所有子数组对
for (int l1 = 1; l1 <= n; l1++) { // 枚举第一个子数组的起始位置 l1
for (int r1 = l1; r1 <= n; r1++) { // 枚举第一个子数组的结束位置 r1
ll sum1 = sum(l1, r1); // 计算第一个子数组的和
for (int l2 = r1 + 1; l2 <= n; l2++) { // 枚举第二个子数组的起始位置 l2
for (int r2 = l2; r2 <= n; r2++) { // 枚举第二个子数组的结束位置 r2
ll sum2 = sum(l2, r2); // 计算第二个子数组的和
ans = min(ans, abs(sum2 – sum1)); // 更新最小绝对差
}
}
}
}

cout << ans; // 输出最小绝对差
return 0; // 程序结束
}

逆天题解：（真的想不出来，我是个只会暴力的fw）

#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std; // 使用标准命名空间

const int N = 1e3 + 10; // 定义常量 N，表示数组的最大大小
long long a[N]; // 定义数组 a，用于存储前缀和
int n; // 定义整数 n，表示数组的大小
multiset<long long> s; // 定义 multiset，用于存储所有可能的子数组和

// 自定义函数，返回两个数中的较小值
long long minn(long long a, long long b) {
if (a < b) return a;
else return b;
}

int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 取消同步流，加速输入输出
cin >> n; // 输入数组的大小 n

// 读取数组并构造前缀和
for (int i = 1; i <= n; i++) {
cin >> a[i];
a[i] += a[i – 1]; // 计算前缀和
}

// 枚举所有可能的子数组和，并将其插入 multiset
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j++) {
s.insert(a[j] – a[i – 1]); // 计算子数组 [i, j] 的和，并插入 multiset
}
}

long long res = 1e9; // 初始化结果为一个大值（1e9），用于存储最小绝对差

// 遍历所有可能的第一个区间的右端点 i
for (int i = 1; i < n; i++) {
// 删除以 i 作为右端点的所有子数组和
for (int j = i; j <= n; j++) {
auto k = a[j] – a[i – 1]; // 计算子数组 [i, j] 的和
s.erase(s.find(k)); // 从 multiset 中删除该和
}

// 遍历所有可能的第一个区间的左端点 j
for (int j = 1; j <= i; j++) {
auto k = a[i] – a[j – 1]; // 计算第一个子数组 [j, i] 的和

// 在 multiset 中查找最接近 k 的值
auto p = s.lower_bound(k); // 找到第一个 >= k 的值
if (p != s.end()) {
res = minn(res, abs(*p – k)); // 更新最小绝对差
}
if (p != s.begin()) {
p–; // 找到第一个 < k 的值
res = minn(res, abs(*p – k)); // 更新最小绝对差
}
}
}

cout << res << endl; // 输出最小绝对差
return 0; // 程序结束
}