【leetcode刷题日记】lc.73-矩阵置零

目录

1.题目

2.代码

1.题目

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

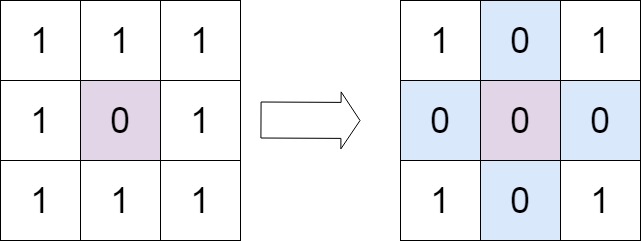
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

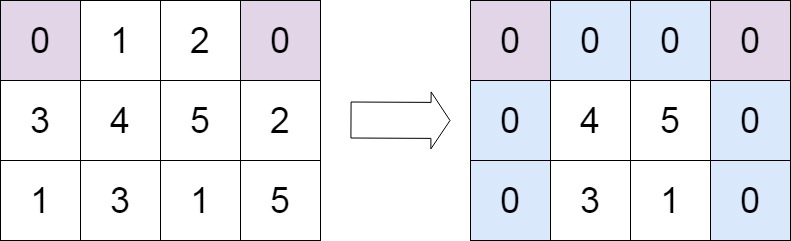
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 – 1

进阶：

• 一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

2.代码

class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
std::vector<bool> rows(m, false);
std::vector<bool> cols(n, false);

// 记录哪些行和列中存在值为 0 的元素
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 0) {
rows[i] = true;
cols[j] = true;
}
}
}

// 根据记录的信息将相应的行和列置为 0
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (rows[i] || cols[j]) {
matrix[i][j] = 0;
}
}
}
}
};